Modelos do campo gravitacional da Terra têm falha fundamental

Com informações da Physics World - 23/07/2024

O estratovulcão Chimboraço é a montanha mais alta do Equador, mas é também a mais alta do mundo se a medição for feita do seu topo até o centro da Terra.
[Imagem: Dabit100/ David Torres Costales Riobamba]

Mapa da gravidade da Terra

Fazer um mapa da gravidade da Terra é algo mais difícil do que parece, já tendo sido objeto de pesquisas feitas a partir do solo e do espaço.

Assim, os modelos computadorizados se tornam elementos importantes. Contudo, mesmo aqui, antes é necessário construir modelos confiáveis.

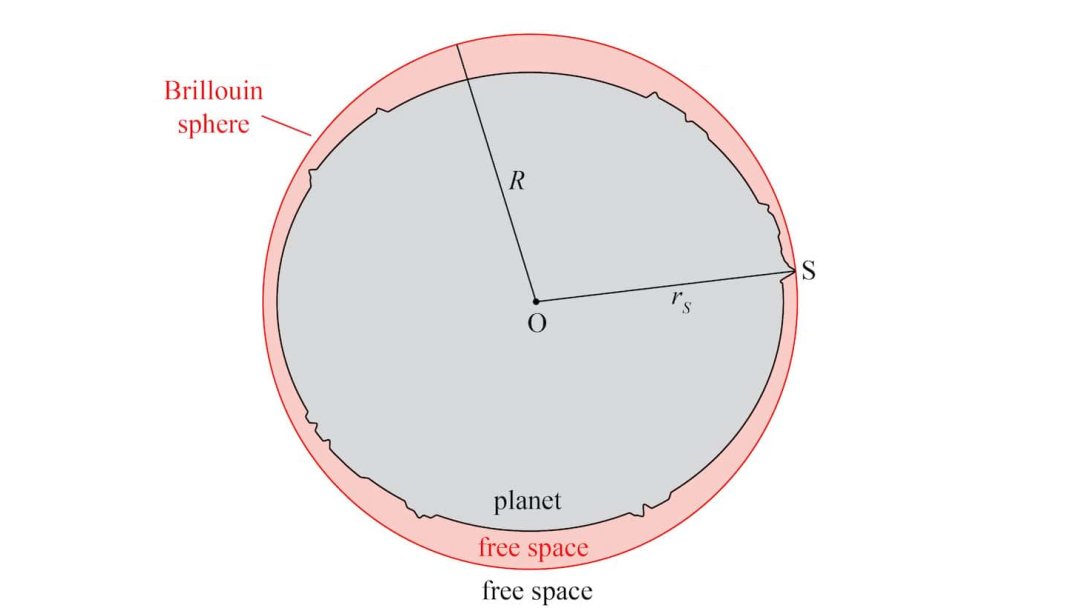
Se a Terra fosse uma esfera ou elipsoide perfeita, modelar seu campo gravitacional seria fácil. Mas não é, então os geocientistas usam um modelo aproximado baseado na chamada esfera de Brillouin, que é a menor esfera geocêntrica onde cabe todo o planeta, tocando a Terra em um único ponto. Talvez você pense logo no Monte Evereste (8.848 metros), mas na verdade o ponto de maior projeção do nosso planeta rumo ao espaço é o cume do Monte Chimboraço (6.263 metros), no Equador, porque, mesmo sendo mais baixo, ele fica perto da crista do bojo equatorial da Terra.

Para o ponto que toca a esfera de Brillouin, os métodos tradicionais, baseados em expansões dos harmônicos esféricos (HE), produzem uma boa aproximação do campo gravitacional real da Terra. Mas, para pontos dentro da esfera - isto é, para todos os lugares na superfície da Terra ou perto dela abaixo do pico do Monte Chimboraço - essas mesmas expansões HE geram previsões erradas. A propósito, harmônicos esféricos são funções que representam a variação espacial de um conjunto ortogonal de soluções da equação de Laplace, quando a solução é expressa em coordenadas esféricas.

Uma equipe de físicos e matemáticos das universidades do Estado de Ohio e Connecticut, nos EUA, investigaram agora a diferença entre as previsões do modelo e o campo gravitacional real da Terra.

Eles descobriram que as equações de expansão HE divergem abaixo da esfera de Brillouin, levando a erros. A equipe também quantificou a escala desses erros.

Zona de divergência: Uma seção que passa pelo centro de massa (O) de um planeta e o ponto único (S) na superfície do planeta que toca sua esfera de Brillouin. O ponto O é o centro da esfera de Brillouin e a origem do sistema de coordenadas no qual se expressa a expansão dos harmônicos esféricos (SHE) do potencial gravitacional (V). S tem a maior coordenada radial (r) de qualquer ponto da superfície do planeta, convergindo no espaço livre sobre ou acima da esfera de Brillouin, mas divergindo no espaço livre abaixo da esfera de Brillouin. A zona rosa é, portanto, a zona de divergência.
[Imagem: M. Bevis]

Implicações para a navegação e os exoplanetas

Os pesquisadores demonstraram que o erro de previsão baseado na divergência aumenta exponencialmente com a profundidade abaixo da esfera de Brillouin.

"Além disso, em um determinado ponto do espaço livre abaixo da esfera, descobrimos que o erro de predição diminui à medida que o grau de truncamento N aumenta em direção ao seu valor ideal, Nopt," explicou o professor Michael Bevis. Além deste ponto, entretanto, "aumentar ainda mais N fará com que as previsões do modelo se degradem, [e] quando N >> Nopt, o erro de previsão crescerá exponencialmente com o aumento de N."

A consequência prática mais importante disto é que que agora é possível quantificar o efeito desse resultado matemático na precisão da previsão de qualquer modelo gravitacional formado a partir de uma chamada expansão HE truncada - ou polinômio EH - em qualquer lugar, na superfície da Terra ou perto dela.

O trabalho mostra que os modelos tradicionais do campo gravitacional terrestre são fundamentalmente falhos quando aplicados em qualquer lugar próximo da superfície do planeta, o que ocorre porque eles estão tentando representar uma quantidade física definida com uma série que na verdade diverge localmente.

Isso irá ajudar os pesquisadores a formular e validar uma próxima geração de modelos gravitacionais globais, o que tem implicações importantes para a navegação inercial e até para a astrofísica dos exoplanetas. Nesta última linha, a equipe já está trabalhando para melhorar a precisão do seu simulador de gravidade para que ele possa modelar melhor planetas com densidade interna variável e topografia mais complexa.

Mais tópicos